北航2025面向对象第一单元

[toc]

第一次作业

1.代码架构分析

在阅读往届学长的博客（以及尝试使用正则表达式解析嵌套括号）后，最后决定了使用递归下降算法。最最主要的是今年oop中也出现了递归下降方法，课程写的文档挺不错的，通俗易懂。找了一下，发现居然也是一位学长的博客

虽然只学了一年多编程，但是苯人对递归式的函数还是有较深的体会的，主要针对一下两点来写递归函数即可

  • 函数的职责：即明确一个函数返回值或者是函数调用的时机，实际上就是牢记函数初衷（parseExpr就返回表达式，在解析表达式时调用），当描述一个递归函数的递归调用过程中卡壳了，不妨回到这个函数被设计之初的职责，跳出细节才能看到全局。
  • 函数终止的条件：尤其是自调用的递归函数，常常会陷入无限调用的套娃中。使用一个具体的例子往往能够更加好地理解什么时候函数递归到达终点了。

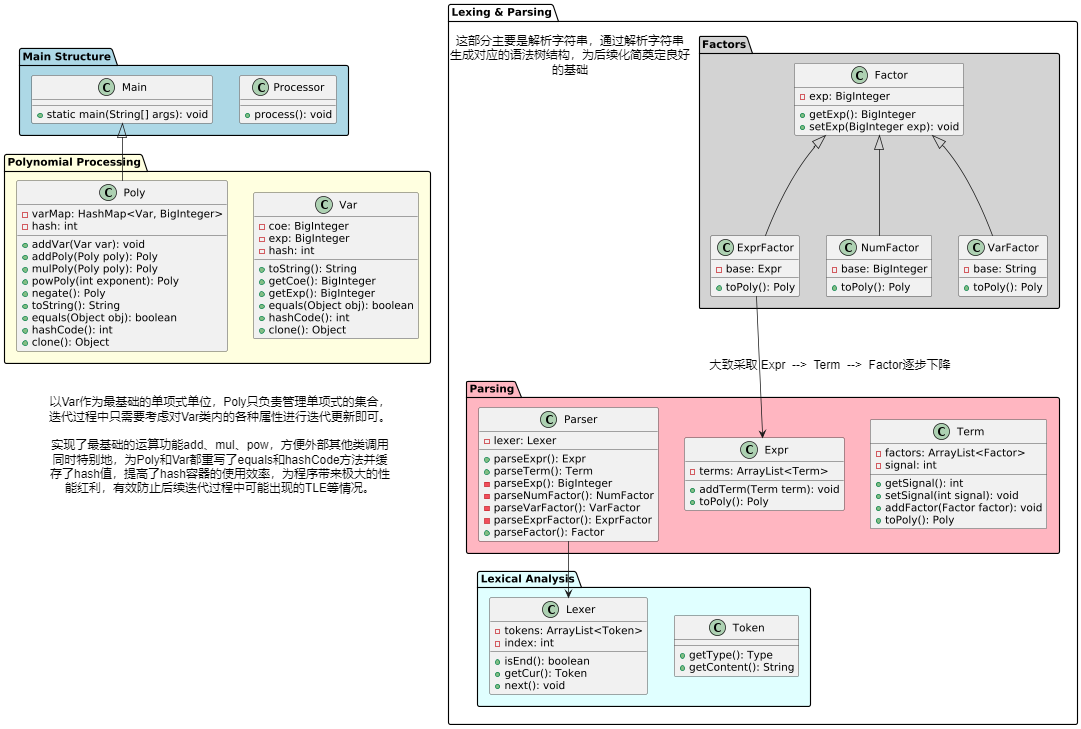
alt text

2.流程分析

我将整个流程分为四个模块，**预处理 -> 解析 -> 合并项 -> 生成字符串**

  • 虽然在本次作业中，生成和优化字符串同隶属于最后一个模块，随着基项复杂度的增加，二者的分开也是在所难免

i.预处理

由于题目给出的原字符串无用信息过多，并不能很好的划分为清晰的Token，所以需要先对表达式进行一些处理

  • 去除空白字符：.replaceAll("[ \t]", "") / .replaceAll("\\s+", "")
  • 合并连续的加减号
    • 使用正则表达式循环替换++ +- -+ --，直到字符串长度不再改变
    • 顺序遍历字符串，记录连续的符号，手动消除

还可以进行的操作，比如去除正号与前导零replaceAll("^\+?0*([0-9]+)$", "$1")好像也不需要其他操作了，当然我没有在预处理阶段处理符号和前导零

ii.解析

按照parseExpr -> parseTerm -> parseFactor

  • 当然，在其中还可以适当封装一些其他方法，降低方法的复杂度
  • 如，三种不同的因子分别使用方法识别parseXXXFactor
  • 识别指数（或缺省）parseExp
  • 总之，方法在保证结构完整、功能集中的情况下复杂度尽可能低

使用递归下降即可，最后得到一个Expr的表达式对象

  • 注意+/-分割，由于我没有在识别Token时将符号与数字一起判断，+/-可能作为项之间的分割也可以作为符号，只要注意在parseTerm、parseFactor注意它们不同的含义即可
  • BigInteger支持解析前导零的字符串，所以这里不用在意了

iii.合并项

在语法树的层面上，我们解析的操作实际是建立了一个庞大的树结构，接下来该应该根据语法树来还原多项式

  • 边建树边返回多项式边化简，此时parse方法的返回值直接改为多项/单项式。优点是效率更高，缺点是依托于强大的算法基础，而且容易错。以Poly、Mono举例

    • parseExpr/parseTerm/parseFactor: Poly：返回表达式/项/因子对应多项式
    • parseExpr将所有parseTerm得到的多项式加起来
    • parseTerm将所有parseFactor得到的多项式乘起来
    • parseNumFactor: 返回纯数字组成的多项式，但是只有一个项[coe * x ^ 0]
    • parseVarFactor: 返回纯自变量组成的多项式，但是只有一个项[1 * x ^ exp]
    • parseExprFactor/parseExpr: 返回表达式因子组成的多项式，但是只有一个项[coe1 * x ^ exp1, coe2 * x ^ exp2, ...]

  • 建树之后后序遍历，为每一种类设置一个返回多项式的函数toPoly作为遍历函数

    • 对于Expr类，先遍历所有子结点也就是Term
      //Expr.java
      public Poly toPoly() {
          Poly res = new Poly();
          for (Term term : this.terms) {
              res.addPoly(term.toPoly());
          }
      }
    • 对于Term类，也先遍历所有子结点也就是Factor
      //Term.java
      public Poly toPoly() {
          Poly res = new Poly();
          for (Factor factor : this.factors) {
              res.mulPoly(factor.toPoly());
          }
      }
    • 其他所有细节都同上
防御性编程
a.“不可变类”

java中有专门的一种类，被称为不可变类，这种类一旦被创建内部属性无法更改。利用了java的机制维护了类内属性的安全性，例如BigInteger或是Integer类都是不可变类

BigInteger tmp = BigInteger.valueOf(2);
// 创建一个存储2的大数

// 实现int类型的自加操作
// tmp++ ???
tmp.add(BigInteger.ONE)
// 发现tmp的值并没有发生改变

tmp = tmp.add(BigInteger.ONE)
// tmp顺利加1，但是tmp并非原来的存储2的对象

而我采用的“不可变类”实际为可变类型，即在创建后是可以被改变的，但是我在编写代码时遵循“协议”（欸欸欸，就是这么高级），人工维护类的不可变性

  • ==类创建的对象在投入使用后属性不可以被改变==，被使用前随意
  • 此处被使用可以理解为参与合并同类项，以Poly对象的使用为例
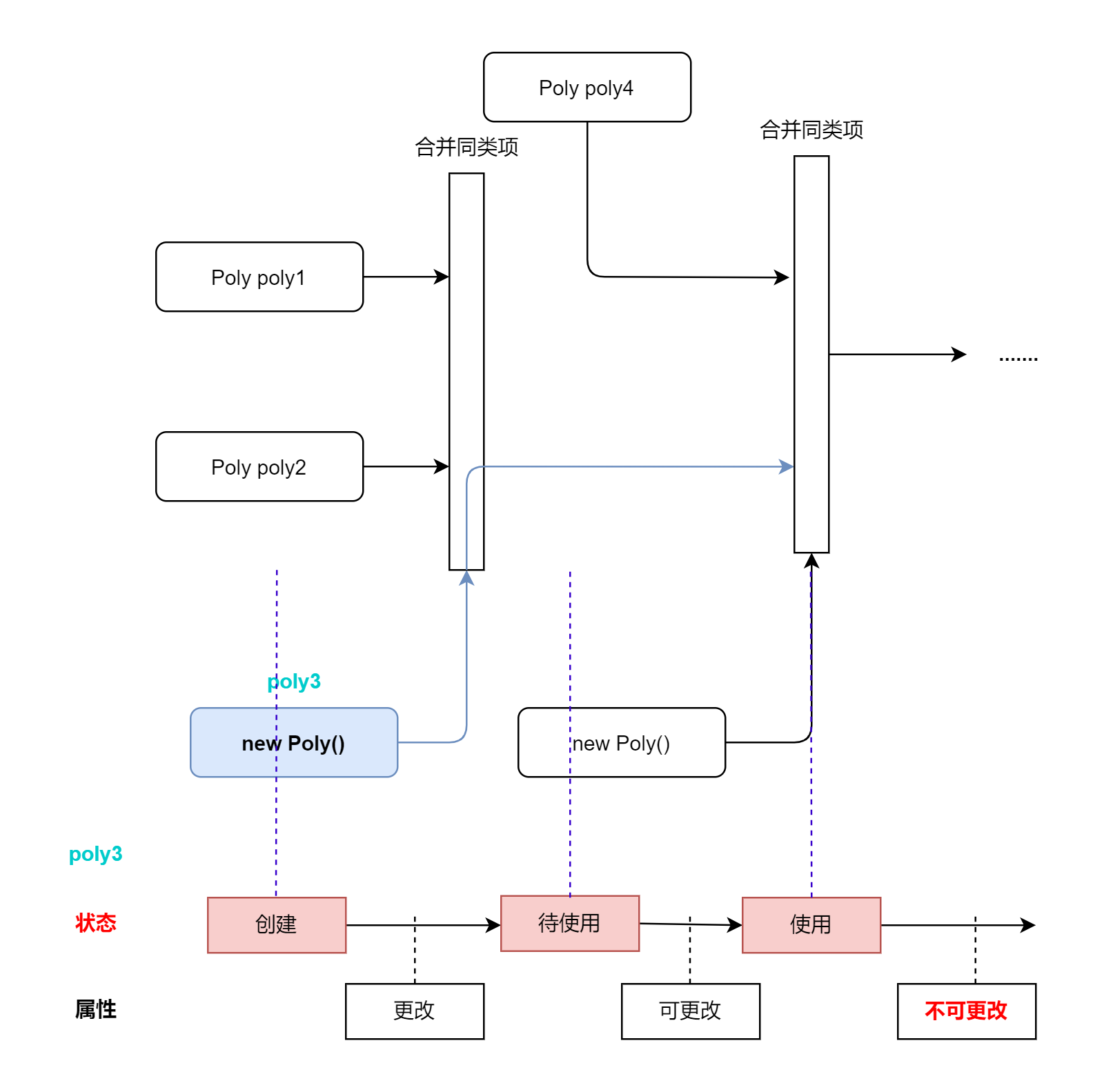
    合并同类项示意图
    • 这里以poly3对象为例，在第一次合并同类项之前，poly3已经被创建，作为接受合并同类项的容器，==此时poly3的内部属性显然在一直改变==（因为单项式一直被加入这个容器）
    • 直到合并同类项完成后一直到使用前poly3都保持一个稳定的状态（==但是此时修改poly3的属性我认为仍然符合我的定义==）
    • 最后当poly3投入合并同类项时，其已经在/被使用了，==此后应该保证poly3属性永远不再改变==
b.克隆
传递方式 描述 使用场景
值传递 实例对象栈上开辟空间，栈存储内容为值，传递时将存储的值给出 简单类型(int char…)
引用传递 实例对象堆上开辟空间，栈存储内容为地址，传递时传递将地址给出 复杂类型(一般JavaBin类)
克隆方式 描述
浅克隆 地址与原对象不同，实例对象内简单类型重新创建，复杂类型传递引用
深克隆 地址与原对象不同，实例对象内简单类型重新创建，复杂类型递归创建新的实例

发现往年有许多学长提出遇到深浅克隆的问题，但是他们大都采取了深克隆的方式较为保险的操作。但是若Poly类与Var类深度耦合，你中有我，我中有你。深克隆该如何进行？

//Poly.java
//HashMap<Var, BigInteger> varMap
@Override
public Object clone() {
  Poly res = new Poly();
  for (Var var : varMap.keySet()) {
    res.addVar((Var) var.clone());  
  }
  return res;
}

//Var.java
//BigInteger coe
//BigInteger exp
@Override
public Object clone() {
  return new Var(coe, exp);
}

将深克隆实现为递归形式，在后续迭代过程中也可以很好的解决Poly与Var之间的耦合关系。例如，为Var类新加一个Poly的属性，我们只需要微调即可。分析可以发现，这并不是一个无限递归的函数，在varMap为空时整个递归达到底部。
//Var.java
//+ Poly expPoly
@Override
public Object clone() {
  return new Var(coe, exp, (Poly) expPoly.clone());
}

但是递归的终点实在是太长了，深克隆是一笔巨大的开销。故而我们不能困于此，我们更多的程序开销应该用来卷性能（），得益于我们类的设计理念，深克隆实际是可以完全规避的

之所以使用深克隆是为了保护数据的一直性，尤其是在引用这种前提下，一个对象可能有多个引用。此时通过某一个引用的修改可能导致其他引用获取到错误的数据。为此可以将将要修改的对象从里到外复制一遍再使用。

回顾我们的设计，我们的Poly类与Var类在投入使用后属于不可改变的状态，自然不存在内部数据被修改而导致的若干现象，省下一大笔性能开销

// Poly.java
public Poly(HashMap<Var, BigInteger> varMap) {
  this.varMap = varMap;
}

public Object clone() {
  // HashMap克隆方式也是浅克隆，键值对是引用
  HashMap<Var, BigInteger> newVarMap = new HashMap(this.varMap);
  return new Poly(newVarMap);
}
c.多项式存储

因为我们时常需要合并同类项，因此能否快速找到同类项十分重要。使用HashSet、HashMap这类使用哈希索引的数据结构十分方便，但是需要重写hashCode和equals方法

//Var.java
public int hashCode() {
  return Objects.hash(exp);
  //不需要比较系数
}

public boolean equals(Object o) {
  if (o == this) {
    return true;
  }

  if (!(o instanceof Var)) {
    return false;
  }

  Var var = (Var) o;
  return var.getExp() == exp;
  //同样只需要判断指数，不需要系数
}
  • 对于Var类型实现了以后，使用HashSet<Var>就十分方便了，之所以使用HashMap主要时考虑到判断Poly是否相等时需要考虑系数
    //Poly.java
    //HashSet<Var>
    public boolean equals(Object o) {
      if (o == this) {
        return true;
      }

      if (!(o instanceof Poly)) {
        return false;
      }

      Poly var = (Poly) o;
      return Objects.equals(varSet, var.getVarSet());
      //此方法比较两个Set中的元素是否能满足equals方法
      //根据我们重写的Var的equals方法，其只考虑了指数
      //即2*x+3*x^2与1*x-3*x^2会被判断为相等
    }

    //改为HashMap<Var, BigInteger> 
    //var <-> coe
    return Objects.equals(varMap, var.getVarMap());
    //比较键值对，所以系数作为值被考虑在内
    //即2*x+3*x^2与1*x-3*x^2不同
    tips：由于我们设计的Poly与Var具有投入使用后不可改变的特性，故而我们可以尝试缓存对应的hash值，这样可以减少调用hashCode()的性能开销
...
//cached hashCode
private int hash;

public int hasCode() {
  if (hash == 0) {
    hash = Objects.hash(......);
  }
  return hash;
}

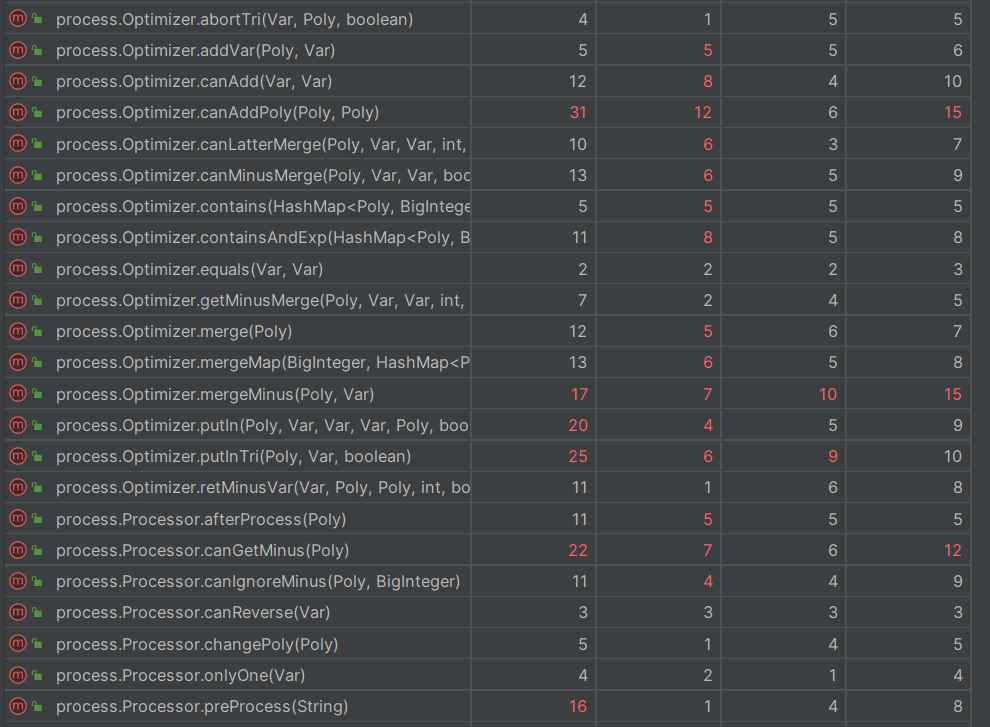
3.复杂度分析

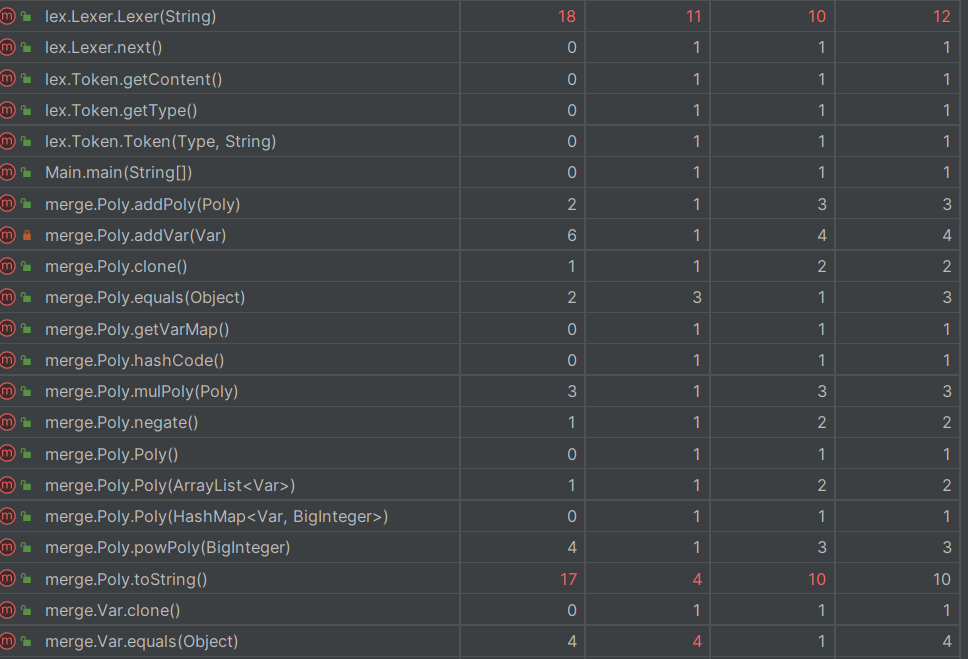
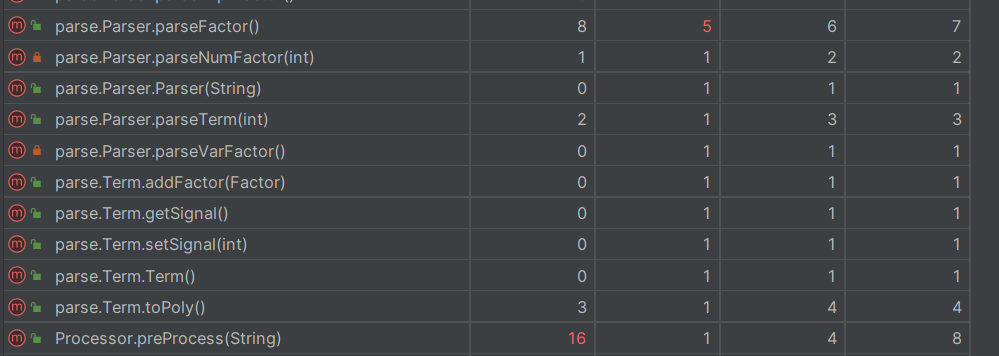
alt text
alt text
这里只列出来爆红的几个方法

  • preProcess里面放了一个合并正负号的循环，复杂度很高
  • Lexer构造方法因为有很多条件分支，导致所有都爆红
  • Poly.toString由于也是有将正数项提前，导致复杂度偏高

4.bug分析

本次作业强测、互测均为出现bug
由于本次作业是第一次迭代作业，主要搭好解析表达式的框架，作业中要求的多项式、单项式的结构也并不复杂，且显然存在最优解，故本次作业细心就不会出现任何问题

  • 构造数据后可以直接使用sympy对拍，对于多项式的处理sympy还是比较擅长的

第二次作业

1.架构设计

就上次作业而言，本次作业新加入递推函数与三角函数因子，难度跨度相较前几年应该是较大，大概是从hw1跳转hw3左右。递推函数实则原先自定义函数+嵌套调用，三角函数内因子类型不限制，化简难度较大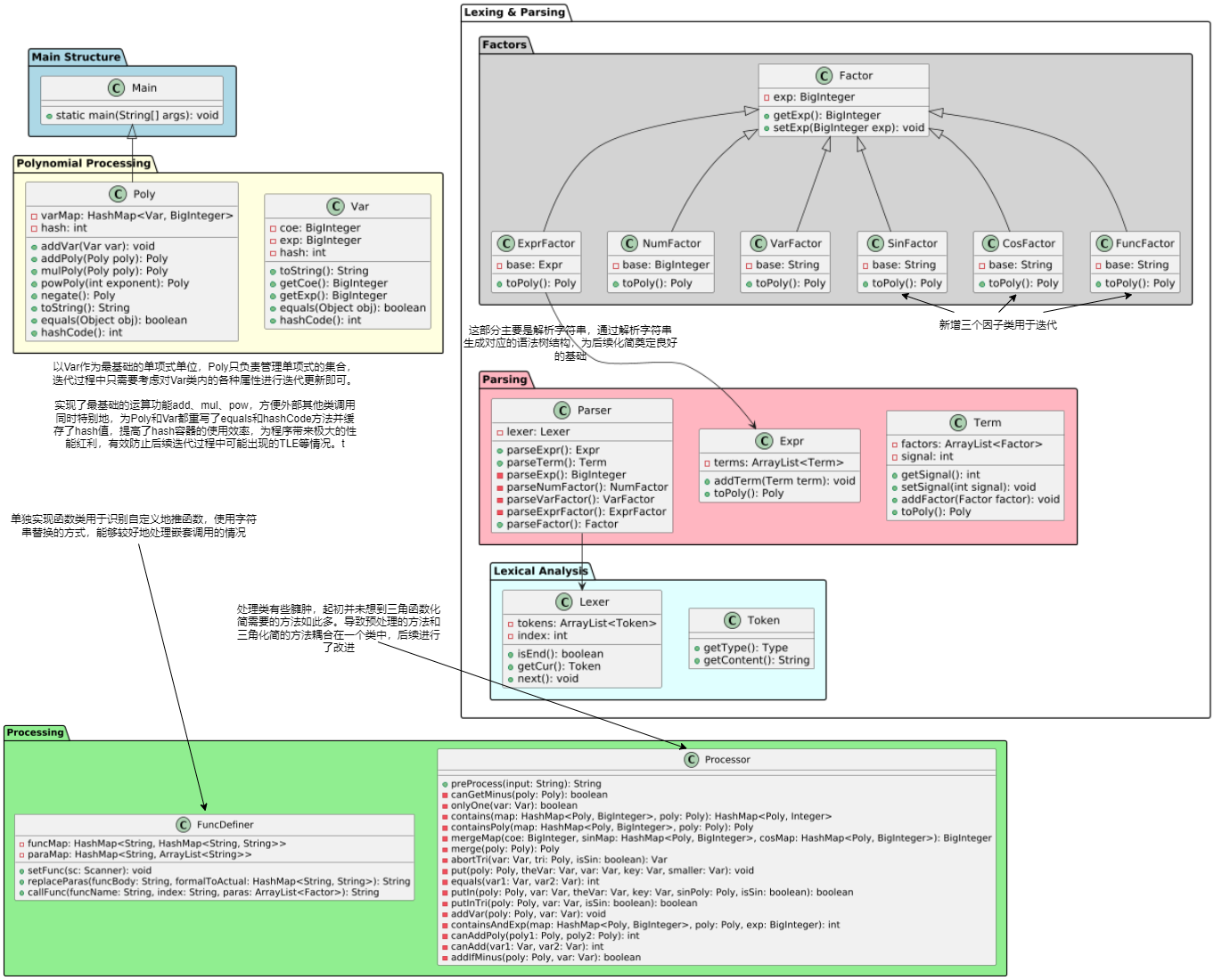
alt-text
(.p.s虽然说字符串替换是陋习，但是在语法树层面的替换容易出现一些神奇的问题，比如形参的实参是形参。。。，除了递归搜索替换也没有其他好的方法)
funcDefiner类

  • 定义为工具类，内部全为静态方法
  • 存储所有递推函数信息（预防迭代）

    • funcMap: HashMap<String, HashMap<String, String>>

      • 将函数名，与调用信息存起来
      • 第一步映射函数名 -> 函数体，为了防止多个递推函数，使用HashMap存储
      • 第二步，针对不同情况下n的取值确定函数体，同样使用HashMap存储
      • f{1}(x...) = ...，递推的基础
        • "1" -> ...
      • f{0}(x...) = ...，递推的基础
        • "0" -> ...
      • f{n}(x...) = f{n-1}(x...) + f{n-2}(x...)，递推公式
        • "n" -> f{n-1}(x...) + f{n-2}(x...)
      • 获取函数f的递推公式 -> funcMap.get("f").get("n")
      • 获取函数g的0的值 -> funcMap.get("g").get("0")

    • paraMap: HashMap<String, ArrayList<String>>

      • 将函数名，与形参列表存起来
      • 函数名 -> 形参列表

    • setFunc(Scanner)

      • 根据传入的n、三个递推式子，收集函数信息
      • 记得预处理，去除空白符号以及可能的连续正负号

    • callFunc(funcName, n, Actualparas)

      • funcName传入此次需要调用的函数
      • n传入此次递归函数的索引值f{3}... -> "3"...
      • 若n不为0 or 1，否则直接使用函数体即可
        • 找到函数体中所有n的位置，根据n位置后的符号与数字替换
        • n=3,f{n-1}(x,y^2)+f{n-2}(x^2,y)
          • f{2}(x,y^2)+f{1}(x^2,y)
      • 将形参替换为实参
        • ActualParas = [Factor1, Factor2] 使用表达式因子，原因在后面，使用Poly对象的toString()，因为有些情况可以化简，如果直接输出可能会卡爆堆
      • 记忆化递归：这里的递归我们funcMap没有存储0,1,n之外的值，事实上我们计算一个表达式的函数体可以先查表例如3，显然不在表内，所以根据f{n}...的递推式计算出f{3}对应的函数体，然后把3加入表内，这样我们的表就变为0,1,3,n了，下次需要使用f{3}时只需要查表即可，不需要重复替换

    • parseFuncFactor

      • 读入函数名、还有此次的n值
      • 读入实参列表时，请使用parseExpr后封装为ExprFactor，因为原有形参可能是幂函数，被替换一次后将不再是因子
      • f{n}(x, y) = f{n-1}(x^2, y) + f{n-2}(x, y^2)
      • 求f{3}((x+1), x)时
      • n=3: (x+1), x实参为表达式因子
      • n=2: (x+1)^2, x; (x+1), x^2出现非因子项，只能使用表达式表示

    • ParaFactor

      • 为了提高封装性，可以新建类代表实参因子，其他同理

2.流程分析

大部分内容和第一次作业是一致的，此处不再赘述，此次作业唯一不同的在于三角函数的化简内容。

三角函数化简

Poly代表多项式类，形如Var1 + Var2 + Var3...
Var代表单项式类，形如$coe\times x^{exp}\times\prod_{i=1}^n{sin(expr_i)^{a_i}}\times\prod_{j=1}^n{cos(expr_j)^{b_j}}$

基于同类项的三角函数化简

什么是同类项

在第一次作业中，单项式的形式极为简单，我们可以认为除去系数，指数相等的单项式就是同类项，即coe1 * x^exp/coe2 * x^exp
在第二次作业中我们引入了三角函数因子，单项式的复杂度急剧上升，甚至由于三角函数本身可以向内或向外传递负号，同类项甚至很难以一种形式化的方式表述出。例如，x*sin(x)与3*x*sin(x)显然是同类项，但是x*sin(x)与3*x*sin((-x))实际上也是同类项，二者同样可以合并。此时判断除系数外的部分相同已经不奏效了，故定义==可加==作为同类项的标准

  • 对于Var类，==可加==意味指数相等，二者的三角函数部分组成的集合（sin、cos）需要满足某种双射，使得双射的两方
    • 三角函数种类相等(同为sin或cos)
    • 三角函数因子的指数相等
    • 三角函数内部的Poly满足可加
  • 对于Poly类，可加意味着，其中的单项式集合满足某种双射，使得双射的两方
    • 可加
    • 将所有可加的Var通过正负号变换为相同格式后，对应的所有Var的系数相同或者互为相反数
  • 举例·
    • x与-2*x是可加的
    • x + sin(x)与-x + sin((-x))是可加的
    • x + sin(x)与-x - sin((-x))不是可加的
    • 2*sin((x-1))^2与3*sin((1-x))^2是可加的
    • x + 2*sin((x-1))^2与x + 3*sin((1-x))^2是不可加的
    • sin((cos((x-1))+1))与-sin((-1-cos((1-x))))是可加的
    • sin((x^2-cos((x-sin((1-x))))^3-cos((x-sin((1-x))))^1+1-sin((cos((x^2-2*x+1))^2-x+1))^2-sin((cos((x^2-2*x+1))^2-x+1))^3))与sin((x^2-cos((-x-sin((x-1))))^3-cos((-x-sin((x-1))))^1+1-sin((-cos((-x^2+2*x-1))^2+x-1))^2+sin((-cos((-x^2+2*x-1))^2+x-1))^3))是可加的

可以比较容易地看出来，==可加==的定义满足一种递归的形式，这主要是因为Poly和Var内部是深度耦合的，其对应的数据结构是递归形式的，所以我们设计的某种算法也应该遵循其结构，体现为递归形式

如何识别同类项

如果觉得递归麻烦的话可以参考后面的近似算法

也许现在我们已经明晰了什么样的结构是==可加==的，是同类项。但是重要的是我们还需要代码能够知道什么样的结构是==可加==的，为此我们专门在优化类中定义两个方法

  • public static boolean canAddVar(Var var1, Var var2)
  • public static boolean canAddPoly(Poly poly1, Poly poly2)

具体实现可以参考以下结构

// 1代表两项可加，且数学意义上同号
// -1代表两项可加，且数学意义上异号
// 0代表两项不可加
public static int canAddVar(Var var1, Var var2) {
    //若指数不同直接返回
    ...
    //若sin集合数目不等直接返回
    ...
    //若cos集合数目不等直接返回
    ...

    //判断双射只能使用循环了
    for (Poly poly : var1.sinMap) {
        //判断var2中sinMap是否有与poly可加的项
        int sign = contains(var2.sinMap, poly)

        //不含则直接返回
        ...
    }

    //同理判断cosMap中是否有
}

public static int containsPoly(HashMap<?,?>sinMap, Poly poly) {
    //首先可以检测sinMap中是否含有key
    sinMap.containsKey(poly)
    //还可以判断是否有poly.negate()
    sinMap.containsKey(poly.negate())

    //若都不存在则可以循环判断是否可加
    for (Poly other : sinMap) {
        //适当剪枝
        ...
        int sign = canAddPoly(poly, other)
    }
}

public static int canAddPoly(Poly poly1, Poly poly2) {
    //判别个数等剪枝
    ...

    int allSign = 1;
    boolean first = true;
    for (Var var : poly1.varMap) {
        
        int sign = containsVar(poly2, var)
        //若不含则直接返回
        ...
        //若符号不符则立即返回
        if (fisrt) {
            allSign = sign;
            first = false;
        } else if (allSign != sign) {
            return 0;
        }
    }
}

public static int containsVar(Poly poly, Var var) {
    //适当剪枝
    for (Var other : poly.varMap) {
        //适当剪枝
        ...
        int sign = canAddVar(other, var)
        //不可加返回
        ...
    }
}
识别同类项加速

由于我们识别同类项的式子是一个递归式，最坏的情况可能接近$O(n)$(还是在剪枝相当不错，可以尽早发现两个式子不是同类项的时候，否则大概是$O(n^{n^{n^{…}}})$，这为我们的程序性能带来了极大的打击。为此我们可以通过一些预处理的手段加速我们识别同类项的速度————尽可能地规定一个范式，因为我们无法判定含三角函数的一大难点就是同类项可能差异巨大，难以通过一般方式识别

对于三角函数内可以提出负号的情况例如sin((-x-1))和sin((-x))，我们可以化简为-sin((x+1))和-sin(x)。而且可以看出这样的提出方式显然是有利无害的

接下来对于有正有负的情况我们到底是提负号还是不提负号呢，答案是比较hash值，其实这样想到主要是因为三角函数内部是Poly，而Poly内部天生的缓存了hash。所以我们可以判断一下Poly和Poly.negate()两个对象那个hash比较大/小（规则统一即可），这样我们可以递归地证明大部分情况下是可以正确处理好同类项的

最后还有一种极为特殊的情况，Poly与Poly.negate()的hash值相等怎么办，那我到底取反还是不取反呢。例如我自己测试时发现cos((x^2-2*x+1))与cos((-x^2+2*x-1))的hash值是相等的，那么此时可以

  • 使用之前的递归判断方式，增大耗时以求最最最准确的答案
  • 放弃优化，认为这种情况出现的概率实在是太低了，前面的方案已经足以应对绝大部分情况而且性能极佳

    如何选择全凭个人，但是追求性能的同时不要忽视正确性和程序运行性能，顾此失彼、因小失大并不是明智的选择
    就像我是选择了最求最最最准确的答案，并对一些极端情况做了测试，效果并不差

如何利用可加项化简

若知道expr1与expr2可加，expr3与expr4可加且同号

  • c * 2^i * sin(expr1)^i * cos(expr2)^i (sin二倍角公式)
    • c * sin(2*expr1)^i
  • c1 * expr3 * sin(expr1)^2 + c2 * expr4 * cos(expr2)^2 (平方和公式变形)
    • 若c1 == c2，c1/c2 * expr3
    • 若c1 > c2，c2 * expr3 + (c1 - c2) * expr4 * sin(expr1)^2
    • 若c2 < c2，c1 * expr3 + (c2 - c1) * expr4 * cos(expr2)^2
  • c1 * expr3 * sin(expr1)^2 - c2 * expr4 * cos(expr2)^2 (cos二倍角公式)
    • 若c1 == c2，- c2 * expr4 * cos(2*expr2)

3.复杂度分析

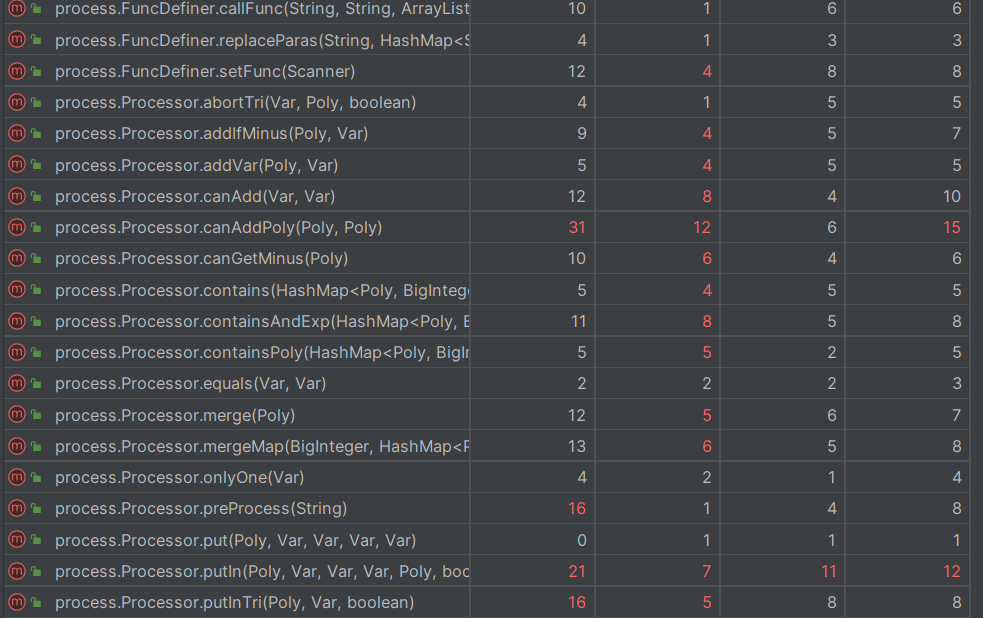
alt text

  • 本次作业的重灾区在三角函数化简部分，由于有大量的剪枝，导致复杂度特别高，看起来较难进一步减少复杂度
  • 其余上次作业的部分有所改善

4.bug分析

本次作业强测、互测均未出现bug

值得一提的是，由于本次作业跨度过大，导致就算是A房也是血流成河。房间里大致发现了9个bug左右。有些人的bug太过简单导致经常输出，最后有效刀16刀，总结一下出现的各类bug

  • 自定义递推函数形参替换问题，使用replace替换两遍，这对于f(x, y)是没有问题的，但是对于f(y, x)会导致形参y的实参中的x再次被错误替换
  • 错误判等条件，有同学的Poly类相等方法是return hashCode() == poly.hashCode()，这个错误是显然的，这位同学并没有考虑hash冲突的情况
  • 输出调试信息，有一位同学在三角函数化简时会输出extra ....的调试信息
  • 格式问题，有同学在化简括号过程中sin(-2*x)必要括号未保留
  • 符号处理不到位，有位同学一边建树一边化简，由于保留符号的地方太多而混淆，导致识别正负号有问题

惨烈的hw2（），有点可惜的是在周六上午还想到了可以和差化积化简，但是最后由于下午做志愿打消了这个想法，没想到最后强测性能中真的出现了。故在第三次作业中实现了和差化积

第三次作业

1.代码架构分析

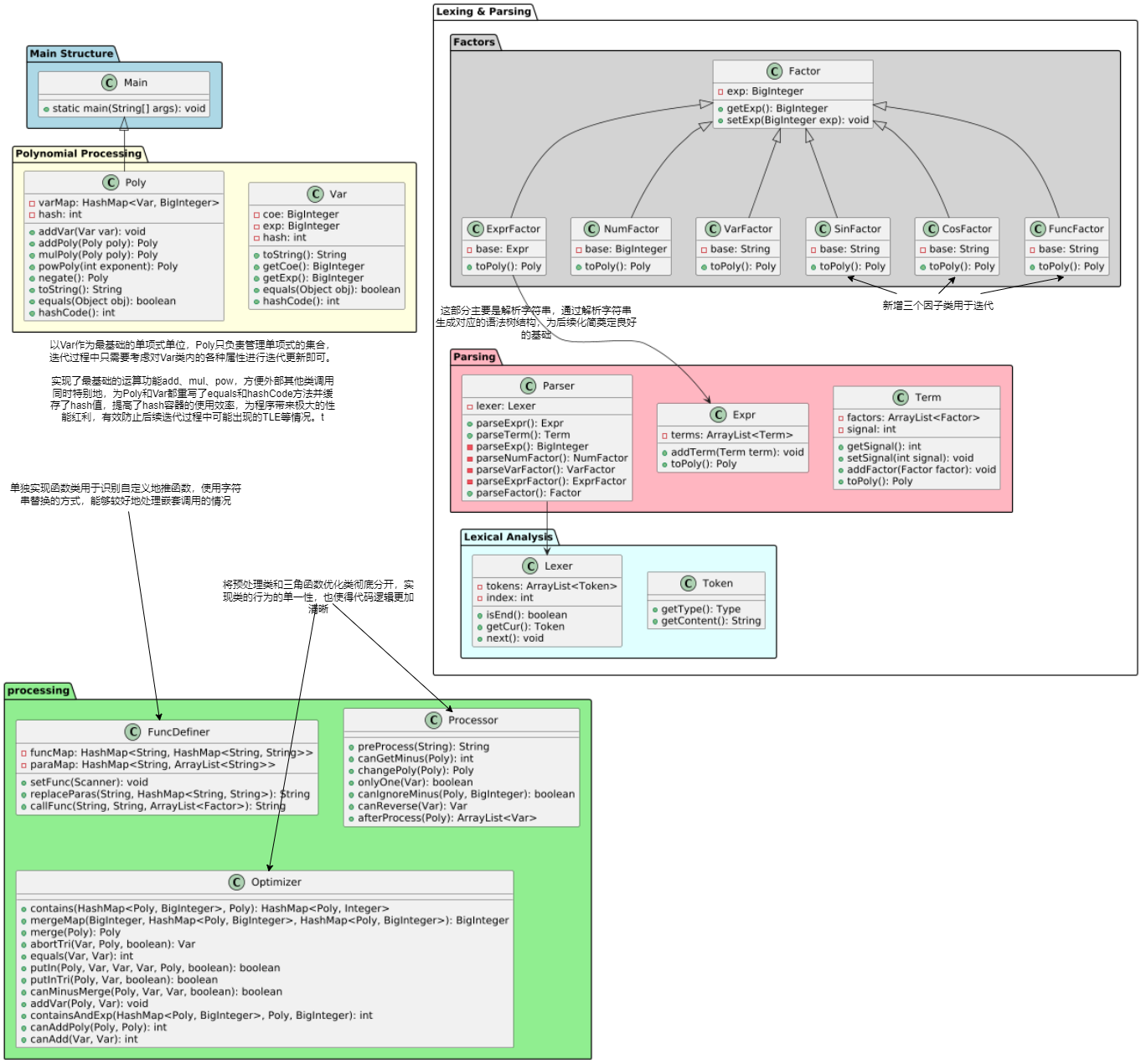
alt-text
本次作业加入了求导因子和自定义函数因子

针对自定义函数，可以单纯理解为一个自定义递推函数，这个自定义递推函数只有初始化的函数体，其他直接套用自定义递推函数

针对求导因子，我将其设置在Poly与Var对象中，因为Poly与Var中已经实现了大部分的化简操作，这样直接对化简完的Poly对象进行求导操作复杂度更低一些，举一个不符合互测限制的例子

2
h(y) = cos(cos(cos(cos(cos(cos(cos(y)))))))
g(x) = sin(sin(sin(sin(sin(sin(sin(h(x))))))))
1
f{0}(x) = cos(cos(cos(cos(cos(cos(x))))))
f{1}(x) = sin(sin(sin(sin(sin(sin(x))))))
f{n}(x) = 1*f{n-1}(h(x)) + 1*f{n-2}(g(x))
dx(f{5}(x) - f{5}(x) + f{5}(x) - f{5}(x) + f{5}(x) - f{5}(x))
>>> 0

如果求导因子最后返回表达式的话，大概中间会得到一个特别长的式子，大概率会爆堆。但是如果先对内部进行化简会发现里面实际是0，这样可以减少空间占用

将Poly理解为若干Var相加，Var是由多个基本项相乘

  • Poly.derive()方法就很简单了，调用Var.derive()相加即可
  • Var.derive()的实现略显复杂，考虑将Var分为三份x ^ exp、sinMap、cosMap，分别对其求导再运用乘法原则
    • 同理对于sinMap和cosMap内部的Poly运用链式法则即可

2.流程分析

因为第二次作业中化简表达式不彻底，有三个点性能分为0（），早知道就早点实现和差化积了。所以本次作业加入了如下的化简，并且优化了一下平方和公式的变形

如何利用可加项化简(续)

若知道expr1与expr2可加，expr3与expr4可加且同号
expr5、expr6满足可加，expr7、expr8满足可加

  • c * 2^i * sin(expr1)^i * cos(expr2)^i (sin二倍角公式)
    • c * sin(2*expr1)^i
  • c1 * expr3 * sin(expr1)^2 + c2 * expr4 * cos(expr2)^2 (平方和公式变形 + cos二倍角公式)
    • 若c1 == c2，c1/c2 * expr3/expr4(.p.s这个其实是第三种情况的一种剪枝。。。)
    • 若c1 == -c2， c2 * expr4 * cos(2*expr2/2*expr1)^2
    • 否则c2 * expr4 * cos(expr2)^2 --> c2 * expr4 - c2 * expr4 * sin(expr2)^2然后就可以合并同类项了
  • expr1 * sin(expr5) * cos(expr7) +- expr2 * sin(expr6) * cos(expr8) (sin加减)
    • expr1 * sin(expr5 +- expr7)
  • expr1 * cos(expr5) * cos(expr7) +- expr2 * sin(expr6) * sin(expr8) (cos加减)
    • expr1 * cos(expr5 +- expr7)

3.复杂度分析

alt text

  • 同上次，因为三角函数化简需要剪枝的部分实在是太多，导致整片地方都是爆红区。这部分内容极难优化，纯粹是因为三角函数化简操作实在是过分复杂

4.bug分析

本次作业强测、互测均为出现bug
首先值得一提的是，测评机出现了bug，导致无法判别化简式与原式是否相等，本人在互测中因此被砍了两刀，不过最后还是撤刀了。其实这也体现出大家自己搭的测评机判等也是有点问题

cos((cos(x) - sin(x))^3)
cos(cos(x)+2*sin(x)^2*cos(x)-sin(x)-2*sin(x)*cos(x)^2)

不过我认为这是情有可原的，含有三角函数的式子判等本来就相当艰难，在第二次作业的测评机中，我和室友讨论最后决定使用多次随机点数值计算+误差判断的方式判断。且使用了相对误差（避免因为计算数值过大导致的绝对误差过大）、1e-7左右的误差是较好的

但是在第三次作业中发现了一些缺陷，对于部分在0附近突变的函数值，随机点无法很好地去除这些极端点，导致即使是相对误差也会有极大的缺陷。这时陷入了两难的境地，相对误差和绝对误差的效果都很差，所以最后使用的方案是特高精度随机点数值计算+相对误差/绝对误差同时使用

  • 使用了mpmath库，精度到达了小数点后50位（此处dps和下面的1e-15需要互相配合，否则还是会出现误判的情况）
  • 对于函数值小于1e-15的值，误差使用绝对误差
  • 其余使用相对误差

咳咳，还是说说同房同学的bug，本次找到的bug较少（大家都没啥bug加上被刀了心情不太好（差点破金身了）

  • 有同学求导对于负号的处理出现问题，反转多次导致bug
  • 有同学没有考虑到出现h(x, y) = x...这种只出现一个自变量表达式的情况
  • 有同学深拷贝耗时太多，被sin、cos串卡T了（拿一个房间其他人提交上去的样例），我也整了一个，不过因为cost没交上去，后来想回来改的时候发现被刀了:sob:，所以就结束了悲伤的互测环节（
    2
    h(x)=cos(cos(cos(cos(x))))
    g(x)=cos(cos(cos(cos(h(x)))))
    0
    cos(cos(cos(cos(cos(cos(g(g(g(x)))))))))